哈工大（深圳）信息学部计算机科学与技术学院量子信息课题组已毕业博士生易正中的论文《Recursive expansion of Tanner graph: a method to construct stabilizer codes with high coding rate》发表于国际权威物理学期刊Physical review A（中科院2区，IF3.0）。该论文的通讯作者为王轩教授。

论文题目：Recursive expansion of Tanner graph: a method to construct stabilizer codes with high coding rate

论文作者：Zhengzhong Yi, Zhipeng Liang, Zicheng Wang, Jiahan Chen, Chen Qiu, Yulin Wu, and Xuan Wang

作者单位：哈尔滨工业大学（深圳）

论文简介：

量子纠错是实现大规模容错通用量子计算的关键技术之一。现有主流的稳定子码（如表面码、XZZX表面码、三维/四维toric码等）虽然具有较好的阈值和拓扑保护特性，但普遍存在编码率过低的问题。当代码长度趋于无穷时，这些编码的渐近编码率往往趋于零。这意味着在降低逻辑错误率的同时，需要大量额外的物理比特，从而造成巨大的硬件开销。相比之下，在经典纠错领域，经典纠错码如极化码（polar code）和低密度奇偶校验（LDPC）码早已能在保持较高编码率的同时获得接近香农极限的性能。如何在量子领域找到兼顾编码率与纠错能力的稳定子码，仍是亟待突破的重要课题。

研究动机：

本文在之前的工作中提出了Z-TGRE（Z-type Tanner-Graph-Recursive-Expansion code）码，该码在递归扩展Tanner图的基础上构造，能够纠正Pauli X和Y错误，且具有0.5的常数编码率。然而，它无法处理所有Pauli错误。为克服这一限制，本文进一步推广该构造，提出能覆盖X、Y、Z三类错误的XZ-TGRE（XZ-type Tanner-Graph-Recursive-Expansion code）码，并结合超图积的思想，设计出TGRE-HP（Tanner-Graph-Recursive-Expansion Hypergraph Product code）码。

主要贡献：

提出XZ-TGRE码构造方法：

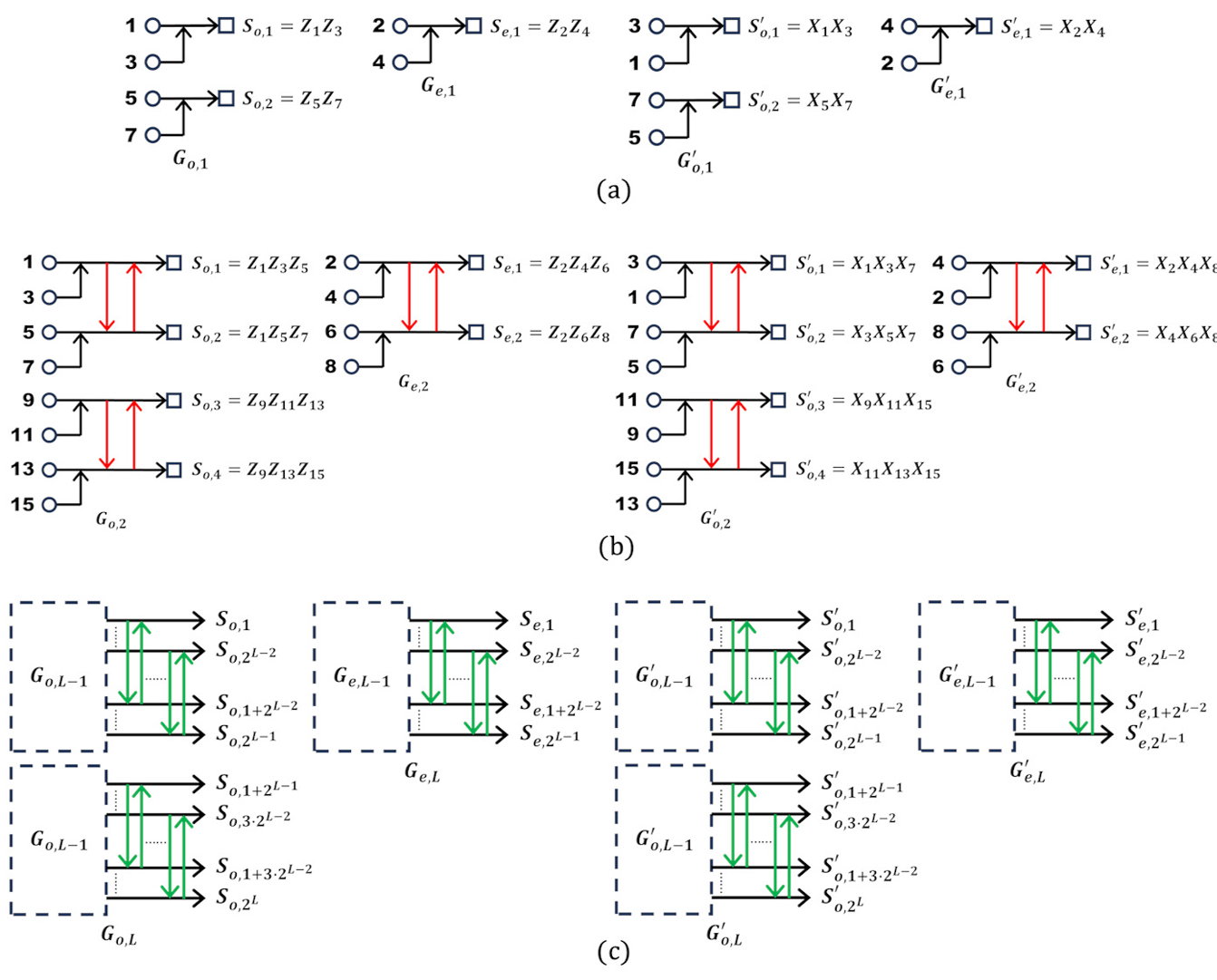
图1 XZ-TGRE码的码字构建方案

码率对比：

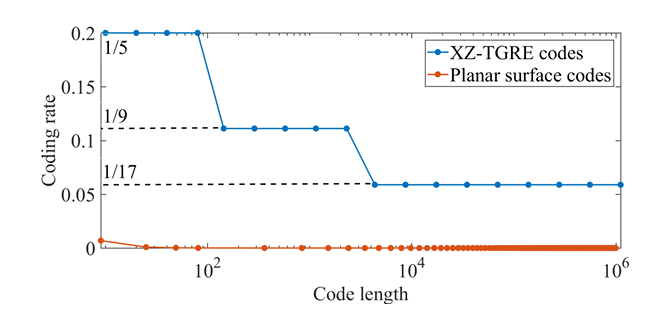
图2 XZ-TGRE码的码率远高于量子表面码

纠错性能：在蒙特卡洛方法和FDBP译码仿真下，XZ-TGRE码的码容量阈值约为0.078，高于(4,5)-双曲面码（阈值约0.025，编码率0.1）和部分四维双曲码。

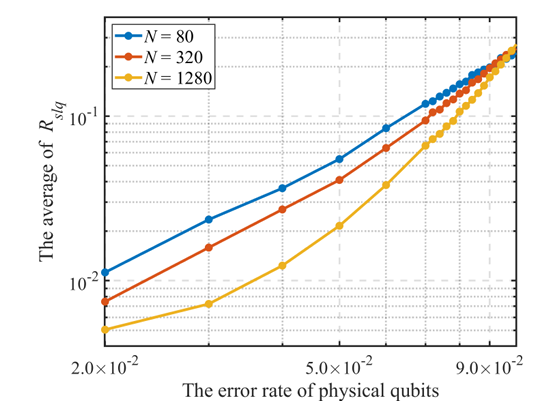
图3 XZ-TGRE码在退极化噪声下取得9.6%的码字容量噪声阈值

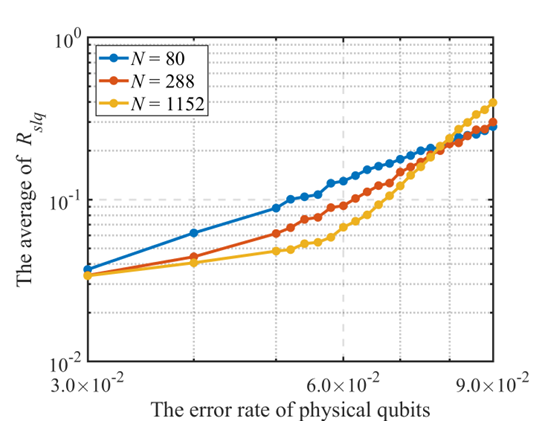
图4 TGRE超图积码在退极化噪声下取得7.8%的码字容量噪声阈值

研究意义:

本文展示了递归扩展Tanner图不仅能产生可纠错单类Pauli错误的量子纠错码，还能设计出对所有类型的Pauli错误都具有纠错能力的量子纠错码。通过超图积方法更是设计出了当前已知码率最高的量子纠错码。本文通过严格的码距证明与数值模拟，展示了新码的实际性能和潜在容错优势。

总结:

本文展示了递归扩展Tanner图作为一种新型量子纠错码构造工具的巨大潜力。XZ-TGRE码和TGRE-HP码在编码率和容错性能之间实现了新的平衡，尤其是TGRE-HP码创下了最高常数编码率的纪录。该工作为解决量子稳定子码“低编码率困境”提供了新的思路，也为未来容错量子计算的硬件实现奠定了基础。

该研究工作获得了深圳市高校稳定支持计划、深圳市基础研究专项和广东省安全智能新技术重点实验室的支持。